理系目線のグラフィックデザイン② 自然の中に潜む数学

今年も2人の日本人科学者がノーベル賞を受賞されました。医学・生理学賞を受賞された大村智氏は、2億人の命を救うとされる薬を開発しました。物理学賞を受賞された梶田隆章氏は、素粒子ニュートリノに質量があることを発見し宇宙の謎に迫りました。これこそクリエイティブだなあとしみじみ感じます。そして彼らの発する言葉には、デザイナーにとっても大切な格言が満載です。
「とにかく科学者は人のためにならなきゃだめだ」
「人のまねをするとそこで終わり。超えることは出来ない」
「最初におかしいと思った瞬間を見逃さずに来れた」
そして最も印象的だったのは大村氏の「すべて微生物の皆様がやっている仕事を勉強させていただいた」。研究対象への敬意・愛・謙虚さに満ちています。私たちデザイナーもデザインへの敬意・愛・謙虚さを忘れてはならないなあと、つくづく思わされました。

さて、ノーベル賞こそ受賞していませんが、それに匹敵する革命的理論を発見したとされる学者がいます。フランスの数学者、ベノワ・マンデルブロです。彼が1975年に提唱した「フラクタル理論」は、いっけんデタラメに見える自然界の形が、ある単純な数式によって説明できるというものでした。

フラクタルとは、その形を拡大しても縮小しても、全体の構造と変わらない「自己相似性」という特徴をもっています。・・・さあ、もう分からなくなってきましたね。例に挙げられるのはカリフラワーの一種のロマネスコです。

小さな円錐が集まって大きな円錐になっています。小さな円錐のひとつを取り出してみても、全体の円錐と印象が同じです。これがフラクタルで、山や雲の形、樹木や河川、海岸線の形状、宇宙に分布する銀河系から稲妻や田んぼの地割れに到るまで、この性質をもっていることが分かっています。これまで自然界の形のほとんどは不規則でデタラメ、偶然できた自由な形と思われていましたが、近年これらにも数学が潜んでいることが分かってきたのです。

自然界のフラクタルを芸術にした例として、マンデルブロは葛飾北斎の「富嶽三十六景　神奈川沖浪裏」を挙げています。小さな波のひとつひとつの形は、大きな波の形と相似形です。もちろん、北斎の時代にフラクタル理論は存在しませんので、北斎の自然を観察する眼がいかに鋭かったかが分かります。

出典：wikipedia

近年では、コンピュータ・グラフィックスの分野でフラクタルを用いて自然の風景を作り出す試みがなされています。「スターウォーズ」や「スタートレック」にもフラクタルは利用されました。自然界には数式が潜んでいる、つまり数式からリアルな自然が作り出せる。・・・しかしCGで作られた自然風景には、まだどこか人工的な感じが残りますね。その隙間には、まだ未発見の数学が存在するのかもしれません。

フラクタルには自己相似性がありますが、実は前回お話しした黄金比にも「小さい長方形を取り出してみても、全体の長方形と比率が同じ」という自己相似性があります。

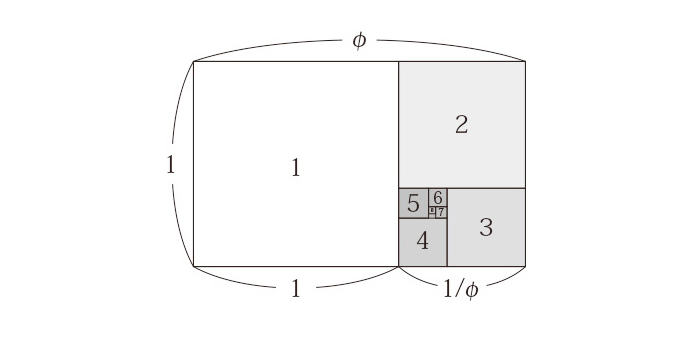
フラクタルと黄金比は実は近い関係にあり、古代から人間が黄金比に魅力を感じてきたのは、そこに自然の原理を見出していた、ということなのかもしれません。人間は黄金比を美しいと感じると言うよりも、自然が作り出す形に美しさを感じる。であれば、私たちデザイナーは美しい形を見分け、生み出していくために、街へ出て商業デザインを見て回るより、もっともっと自然に触れなければいけないのかもしれません。

参考文献：
・三井 秀樹（2000）「形の美とは何か」NHKブックス
・牟田 淳（2010）「デザインのための数学」オーム社